The Split Normal Distribution (or Two-Piece Normal Distribution)

Density, distribution function, quantile function and random generation for the split normal distribution.

Usage

dsplitnorm(x, mode = 0, sd = 1, skew = 0, sd1 = NULL, sd2 = NULL)

psplitnorm(x, mode = 0, sd = 1, skew = 0, sd1 = NULL, sd2 = NULL)

qsplitnorm(p, mode = 0, sd = 1, skew = 0, sd1 = NULL, sd2 = NULL)

rsplitnorm(n, mode = 0, sd = 1, skew = 0, sd1 = NULL, sd2 = NULL)

Arguments

x

Vector of quantiles (for dsplitnorm, psplitnorm).

mode

Vector of modes.

sd

Vector of uncertainty indicators.

skew

Vector of inverse skewness indicators. Must range between -1 and 1.

sd1

Vector of standard deviations for left-hand side. NULL by default.

sd2

Vector of standard deviations for right-hand side. NULL by default.

p

Vector of probabilities (for qsplitnorm).

n

Number of observations required (for rsplitnorm).

Value

dsplitnorm gives the density, psplitnorm gives the distribution function, qsplitnorm gives the quantile function, and rsplitnorm generates random deviates.

Details

If mode, sd or skew are not specified they assume the default values of 0, 1 and 0, respectively. This results in identical values as those obtained from a normal distribution.

The probability density function is: $$f(x; \mu, \sigma_1, \sigma_2) = \frac{\sqrt{2}}{\sqrt{\pi} (\sigma_1 + \sigma_2)} e^{-\frac{1}{2\sigma_1^2}(x - \mu)^2}$$ for \(-\infty < x < \mu\), and $$f(x; \mu, \sigma_1, \sigma_2) = \frac{\sqrt{2}}{\sqrt{\pi} (\sigma_1 + \sigma_2)} e^{-\frac{1}{2\sigma_2^2}(x - \mu)^2}$$ for \(\mu < x < \infty\).

If not specified (via sd1 and sd2), \(\sigma_1\) and \(\sigma_2\) are derived as: $$\sigma_1 = \sigma / \sqrt{1 - \gamma}$$ $$\sigma_2 = \sigma / \sqrt{1 + \gamma}$$ where \(\sigma\) is the overall uncertainty indicator sd and \(\gamma\) is the inverse skewness indicator skew.

Examples

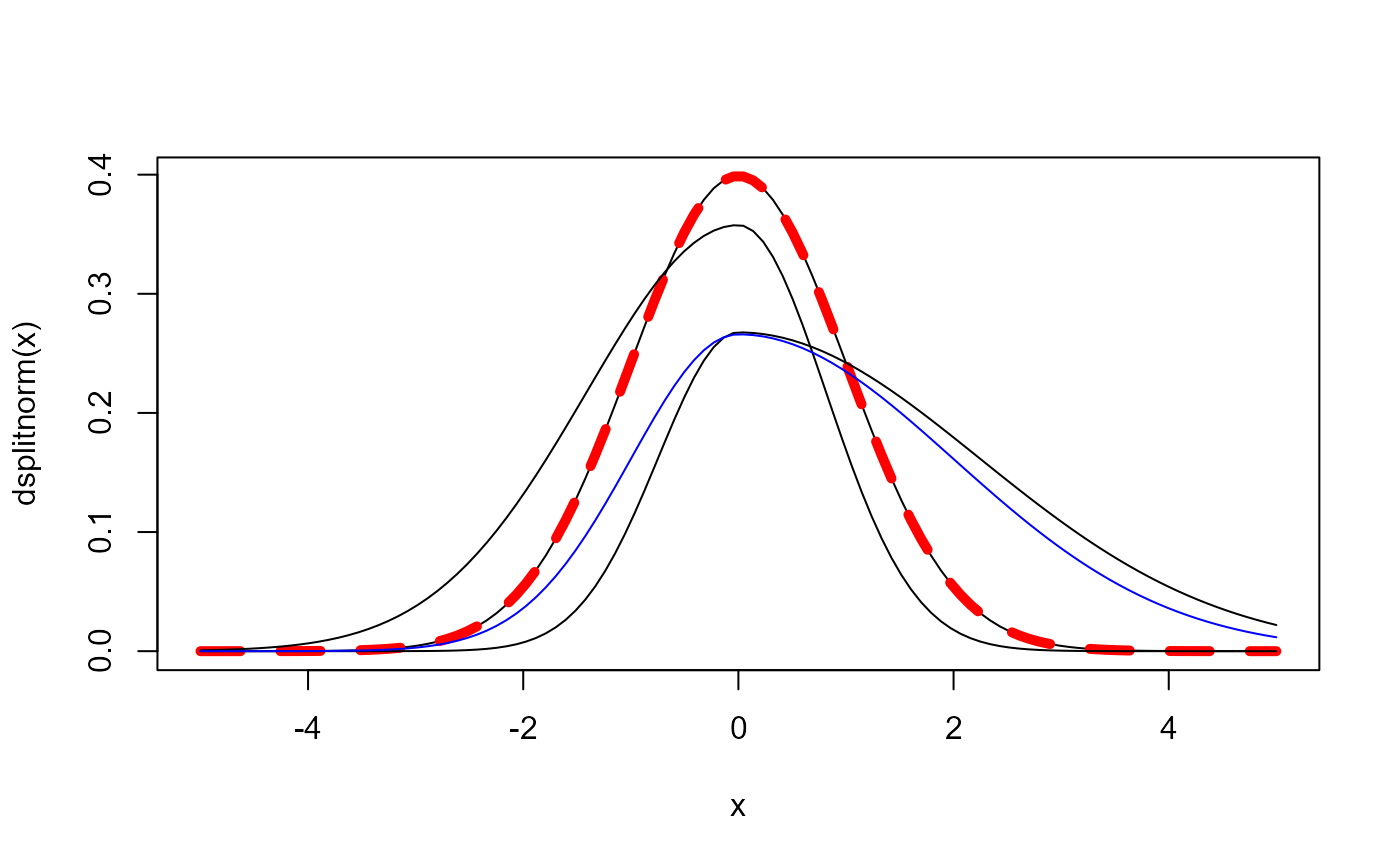
x <- seq(-5, 5, length = 110)
plot(x, dsplitnorm(x), type = "l")

# compare to normal density
lines(x, dnorm(x), lty = 2, col = "red", lwd = 5)

# add positive skew
lines(x, dsplitnorm(x, mode = 0, sd = 1, skew = 0.8))

# add negative skew
lines(x, dsplitnorm(x, mode = 0, sd = 1, skew = -0.5))

# add left and right hand sd
lines(x, dsplitnorm(x, mode = 0, sd1 = 1, sd2 = 2), col = "blue")


# psplitnorm
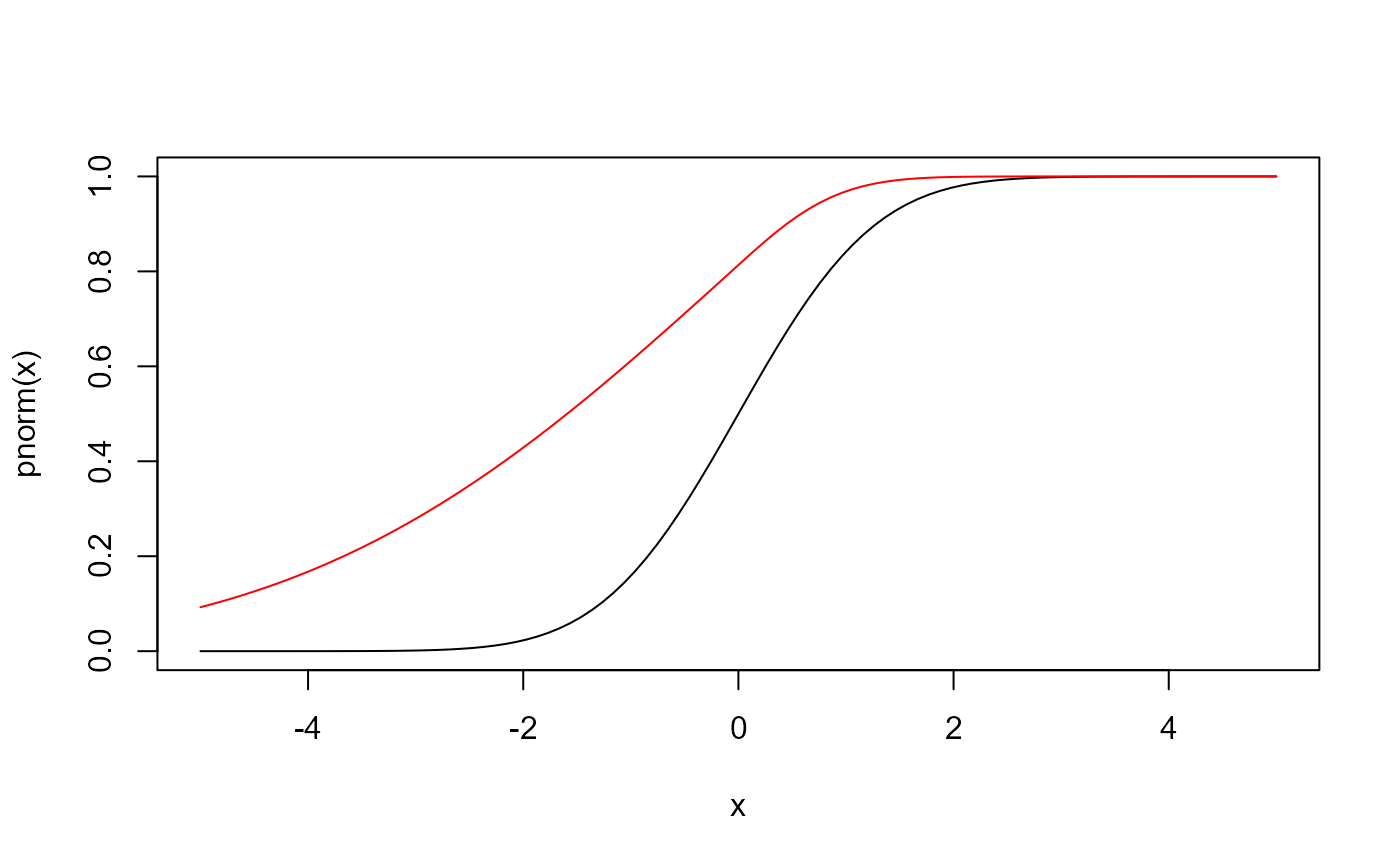
x <- seq(-5, 5, length = 100)
plot(x, pnorm(x), type = "l")
lines(x, psplitnorm(x, skew = -0.9), col = "red")


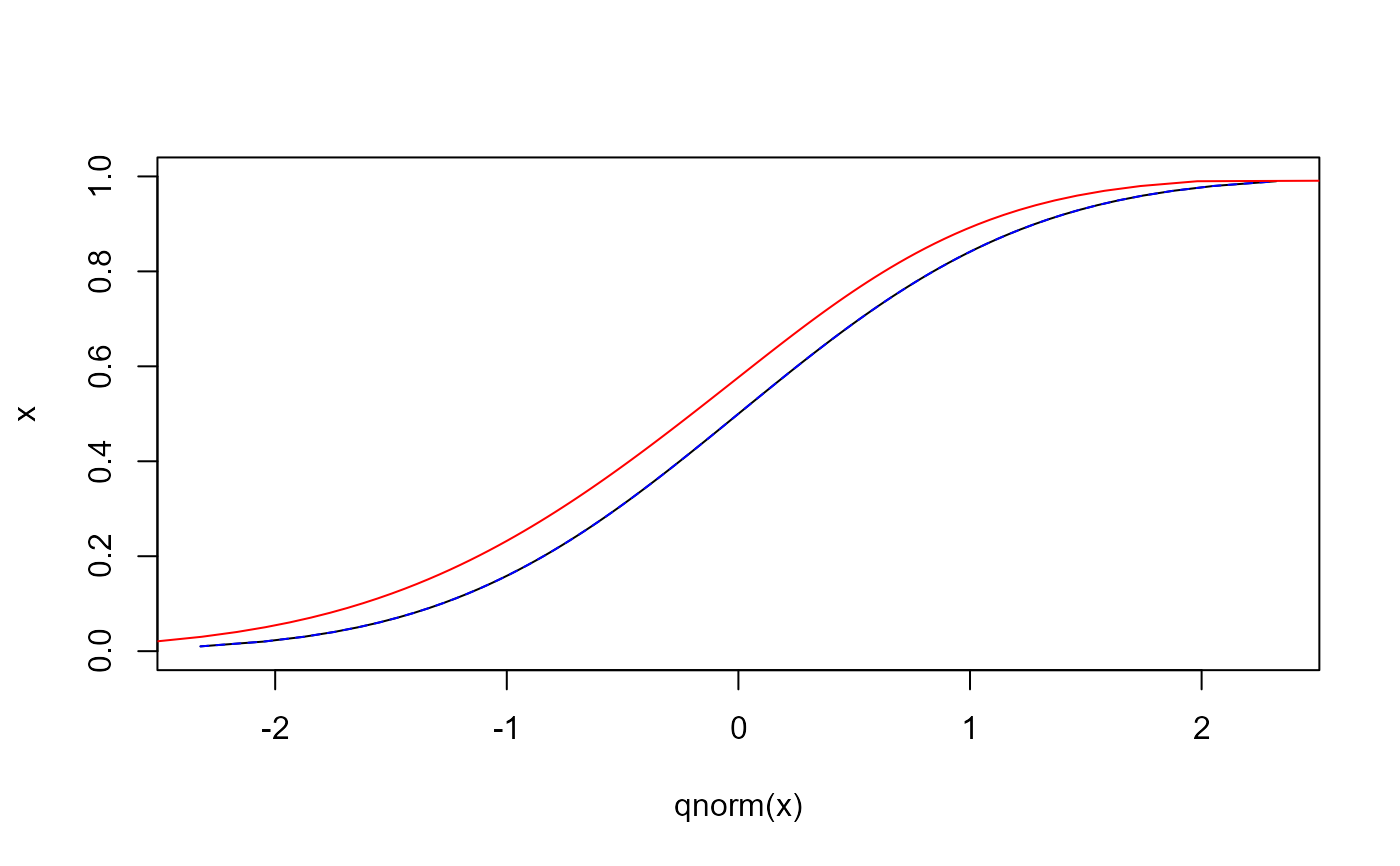
# qsplitnorm
x <- seq(0, 1, length = 100)
plot(qnorm(x), type = "l", x)
lines(qsplitnorm(x), x, lty = 2, col = "blue")
lines(qsplitnorm(x, skew = -0.3), x, col = "red")


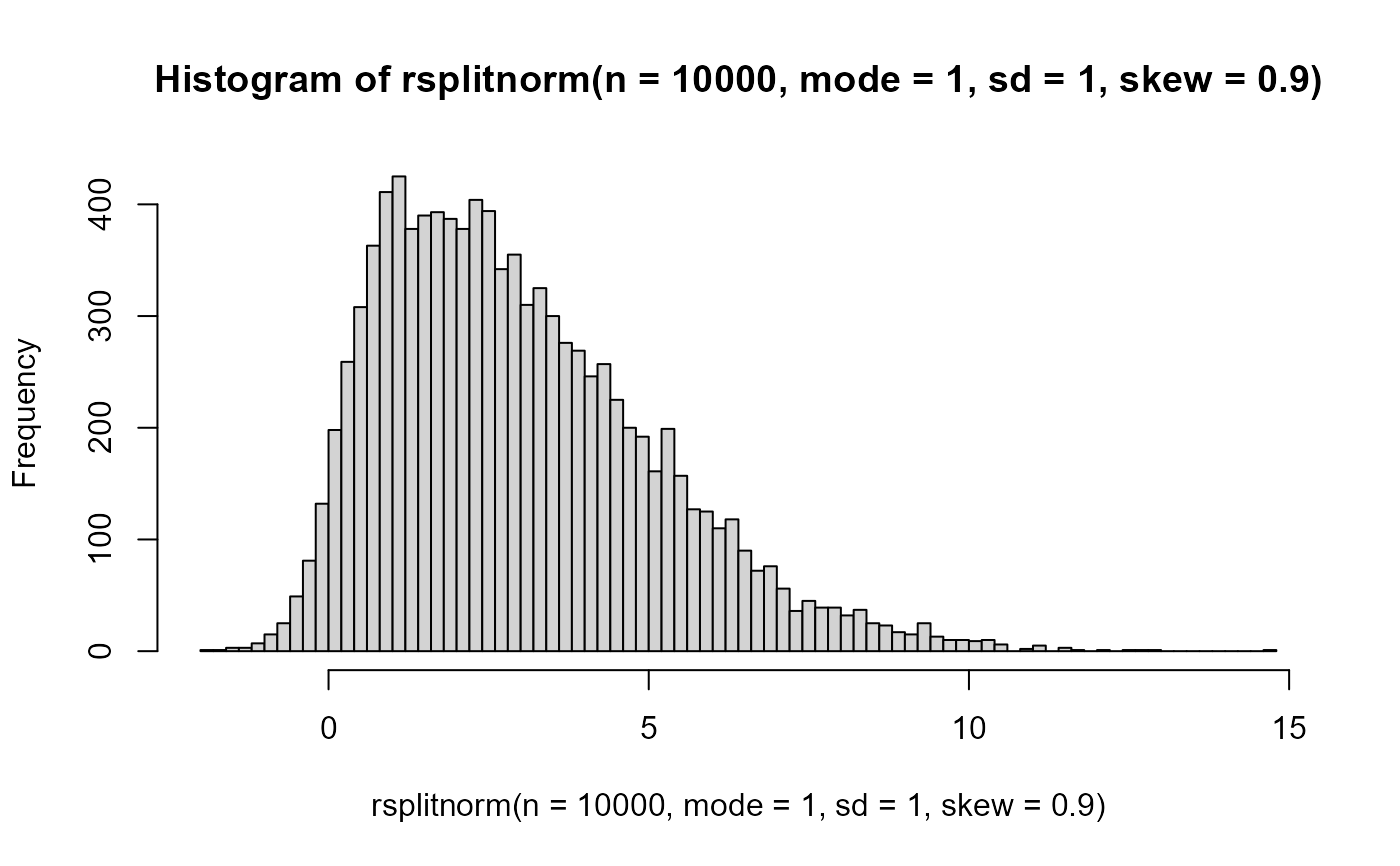
# rsplitnorm
hist(rsplitnorm(n = 10000, mode = 1, sd = 1, skew = 0.9), 100)